作為流體力學中最重要的研究方向，湍流幾乎覆蓋了所有的工程和科研領域。在過去20多年的時間裏，以“湍流”為標題的論文洋洋灑灑，超過5萬篇。而關於湍流的思考和科學研究也已經有了幾百年的曆史，可即便如此，今天的我們仍然沒有辦法給“湍流”下一個准確的定義或結論。

唐太宗曾有言：“以史為鏡，可以知興替”。為了從曆史的角度理解湍流的發展，今天，我們就走近湍流，來一場穿越時空的旅行。

 流體穿越者

關於湍流最早的描述，大概可以追溯到歐洲文藝複興時期。在那個群星璀璨的年代，達·芬奇無疑是最獨特的一個。作為人類曆史上絕無僅有的全才，達·芬奇思想深邃，學識淵博，不僅擅長繪畫、雕刻、建築，還通曉數學、生物、物理、天文等學科。除了《蒙娜麗莎》和《最後的晚餐》等曠世名作之外，達芬奇在自然科學方面也作出了巨大的貢獻。

在流體力學方面，達·芬奇總結出河水的流速同河道寬度成反比，這也是連續性方程最早的描述。他還通過對鳥翼運動的研究，於1493年首次設計出一個飛行器。當然，達芬奇在流體力學領域最大的貢獻仍然是他基於對流體的觀察和思考所繪制的圖畫。

看著達·芬奇創作的流體相關的畫作，感覺仿佛穿越時空一般的神奇。達·芬奇對於湍流細節的掌控，讓人不禁懷疑他在穿越的時候是不是帶了一台能算CFD的電腦。

經典流體力學的叁劍客

藝術和科學在推動人類文明前進中相輔相成。文藝複興之後，整個歐洲的自然科學領域也仿佛開掛了一般，湧現出了諸多屏霸我們物理課本的大神。流體力學的領域自然也不例外。不過為了從科學上解釋和計算流動，大神們選擇性的忽略了達芬奇之前在圖畫中描述的充滿著旋渦的混亂流動，而是選擇研究理想的流體。

作為經典力學的開創者，牛頓大帝當然也沒有放過流體力學。經過大量的實驗研究，牛頓於1686年提出了著名的“牛頓內摩擦定律”——流體的內摩擦力（即粘性力）的大小與流體的性質（粘性系數μ）有關，並與流體的速度梯度和接觸面積成正比。

1738年，丹尼爾·伯努利在經典著作《流體動力學》中提出了著名的伯努利原理：流體速度的增加與靜壓的降低或流體勢能的降低同時發生， 14年以後，丹尼爾一生的摯友——歐拉才給出通用形式的伯努利方程。當然，歐拉大神對於經典流體力學更大的貢獻則是將微分方程應用到了流體力學的領域，並提出了影響後世的歐拉方程，即牛頓第二定律施加到理想流體上的微分方程。

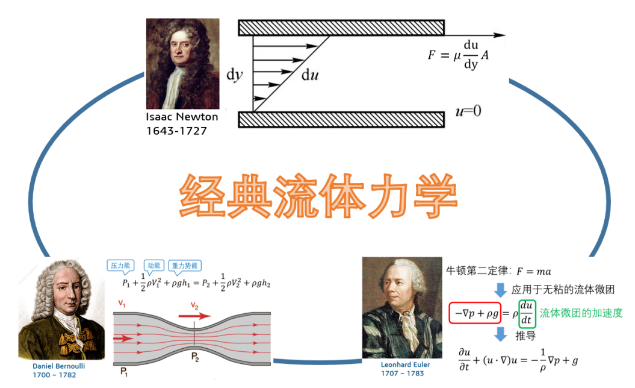
偉大的叁劍客的確把經典流體力學推向了前所未有的高度，但無論是伯努利方程還是歐拉方程在真正的湍流面前似乎都顯得力不從心。

 描述真實流動的N-S雙雄

描述理想流體運動的歐拉方程問世以後，吸引了無數的追隨者，然而人們很快便發現歐拉方程的結果總是和實際不一致，主要原因便是歐拉方程沒有考慮到流體的內摩擦，即粘性對流體運動的影響。

直到1822年，納維公開發表了關於流體運動的文章，從分子運動層面闡述了相對運動產生的分子間作用力，文章提到：從大量的經驗來看，壓力並沒有明顯地影響運動流體各部分之間的分子作用所產生的阻力，而這些阻力來源於相鄰分子的速度大小或方向的差異，即分子間的相對速度。另外，納維在文章中還明確提及了流動的“非線性”，用數學層面的語言解釋了某種混亂的流動。

站在前人的肩膀上，1845年，斯托克斯大展神威，推出了引無數流體人盡折腰的“N-S方程”。作為最普世的流體運動方程，它適用於可壓縮變粘度的粘性流體的運動，當然也適合於湍流。至此，湍流問題的數學描述得以實現。

可是讓流體江湖萬分敬仰的N-S方程卻不是一個省油的燈，正如我們在之前的文章中調侃過的，N-S方程就仿佛流體江湖的“葵花寶典”，所有人都知道修煉成功之後便可縱橫武林，但是欲練此功就必須要“揮刀自宮”。對於N-S方程來說，這最痛的一刀便是方程中的對流項u·▽u，它具有二階非線性，如同一座大山一樣擋在求解者的面前。而非線性本身便是湍流的一大特征。從此N-S方程便和湍流開啟了長達一百多年的糾纏，直至今日。

有一種流動，它有一些任性

深得流體力學俠客們熱捧的N-S方程雖然1845年就面世了，但很長一段時間以來，人們並沒有建立起它和實際湍流流動之間的關聯。於是人們將目光從N-S方程轉向了湍流本身。

法國著名的機械工程師和數學家Saint-Venant首先在公開發表的文章中區分了 “常規”和“動蕩”兩種流動狀態。後來，人們對這兩種流態之間的過渡產生了濃厚的興趣，大家開始尋求一種解釋這種過渡的機制，並尋求一種表征流動不規則、不穩定或者扭曲的標准。

時光荏苒，直到1883年，雷諾通過著名的圓管染色實驗，才向人們展示了湍流無規則的流態：隨著流速的增加，平穩的流動便逐漸演化為雜亂無章的流動，即為湍流。這大概是我們在教科書上第一次遇見湍流的樣子。然而，彼時的雷諾還不知道這種雜亂無章的流動在後世被稱為“湍流（turbulence）”，他也不知道後來有一位量子力學的大神——索末菲用他的名字命名了一個神奇的無量綱數——雷諾數。

雷諾實驗的第二年，雷諾在《Nature》上發表了一篇關於“水的兩種運動方式”的論文，描述了兩種流動狀態之間的過渡，其中有一段比喻很有趣：一支小型部隊很容易在行動中遵守秩序和紀律；而一支龐大的軍隊則更有可能出現混亂。“平穩的流動”類似於一支訓練有素的軍隊，而“彎曲或不穩定的流動”就像是一支處於“鬥爭”狀態的部隊。雷諾在文中用軍隊的規模、行進速度、紀律等來類比影響流動狀態的流動尺度、速度和粘度。當然，在文章中，雷諾還提及了擾動對於湍流觸發的影響。

用湍流命名湍流

雷諾實驗的經典之處就在於通過科學的實驗向人們展示了兩種流態之間的過渡以及它們之間的差異。雷諾使用了扭曲、旋渦、不穩定、橫向流動等等諸多的形容詞形容一種複雜的流動，卻唯獨沒有提到“湍流（turbulence）”。直到威廉姆·湯姆森（William Thomson）在1887年發表的兩篇論文中才首次明確使用“湍流（turbulence）”來定義某種複雜的流動。

威廉·湯姆森研究了傾斜的平面流動，並且在文章中提到，當流動是湍流時，流體內部會產生明顯的幹擾，這種幹擾會產生額外的粘性效應。湯姆森進一步建議將流動的兩種狀態分開，一面是剪切流或層流，另一面，則是湍流或動蕩的流動。這是公開發表的文獻中第一次以“湍流（turbulence）”的名詞來清晰的定義大家熟知的湍流。

或許是湯姆森在流體力學領域的地位還不夠顯赫，他提出“湍流（turbulence）”很長一段時間以後並未得到整個學界的廣泛認可。直到20世紀初，Boussinesq開始在論文中統一使用湍流（turbulence）一詞。隨後，現代流體力學的祖師爺普朗特和他的徒子徒孫們也開始全面使用湍流（turbulence）一詞。再之後，湍流不僅僅成為一個所有人認可的名詞，更是成為了一個專門的研究領域。

湍流問題的數學破局

再次回到湍流問題的數學求解，雷諾實驗讓人們親眼目睹了‘速度’這一物理變量的複雜性，而速度紊亂的時空演化本質上就是N-S方程的實際解，然而湍流本身的複雜性使得N-S方程在求解湍流時顯得捉襟見肘。

不過所幸，對於很多工程問題，我們並不需要完全求解湍流。比如工程上更關心流動的壓力損失和平均速度分布，而非湍流的細節。雷諾實驗五年以後，雷諾才幡然醒悟，既然流動未可知，不妨使用統計學的思想——對N-S方程進行平均，把瞬時速度u分解為時均速度ū和脈動速度u’，代入N-S方程即可得到雷諾平均的N-S方程，也就是RANS。

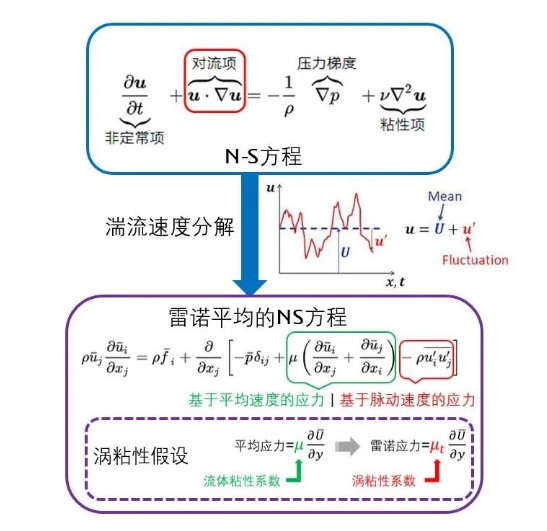
然而雷諾平均的N-S方程似乎更複雜了，除了平均速度的應力，上式中還多了脈動應力項，稱之為雷諾應力，成為新的攔路虎。不過所幸，在雷諾提出對N-S方程進行速度平均的十幾年前，即1877年，Boussinesq 便將湍流脈動引起的切應力類比成了牛頓內摩擦定律，即用粘度乘以速度梯度來表示湍流脈動引起的切應力，也就是雷諾對N-S方程進行速度平均多出來的雷諾應力項。這就是大名鼎鼎的渦粘性假設：雷諾應力=μt*(əū/əy)，其中的μt體現了湍流脈動引起的切應力，稱為渦粘性系數。至此，湍流在數學求解層面出現了真正的破局。

集大成者的開宗立派

盡管雷諾和Boussinesq指明了湍流數學求解的方向，然而道路上卻充滿了沼澤和泥濘，直到咱們的祖師爺——普朗特於1924年提出了混合長度理論，湍流的計算從數學表達到工程應用這座橋梁才逐漸變得清晰。

我們知道流體的粘性來自於分子自由運動產生的摻混，與分子運動自由程密切相關；而對於渦粘性，也可以類似的定義湍流脈動摻混的長度，稱之為混合長度，其物理意義為流體微團耗散前所經曆的距離，因此脈動速度可以表示為混合長度與Y向速度梯度的乘積，而渦粘性系數則可以相應的表述出來。因此，只要知道了混合長度，便可以明確渦粘性系數，進而求解雷諾平均的N-S方程。

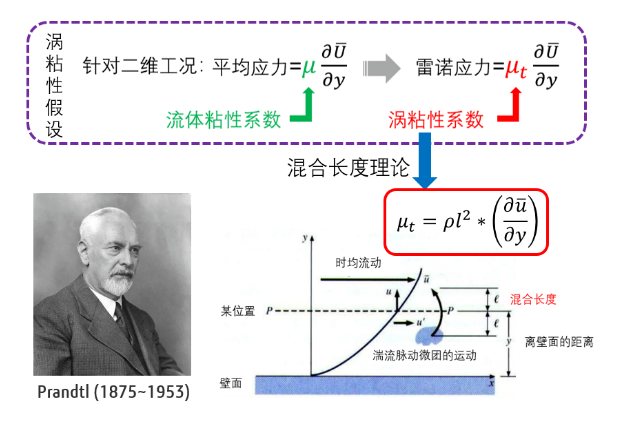
然而混合長度的准確值也很難得知，於是普朗特繼續發揚了“跟著感覺走，天下在我手”的科學精神，大膽的認為混合長度與到壁面的距離成正比，從而得到了CFD領域第一種實用的渦粘模型。1978年， Baldwin和Lowmax基於湍流邊界層內外層的流動差異提出了更合理的B-L模型，即針對湍流邊界層的內層和外層分別定義混合長度。

混合長度模型是代數模型，相當於直接用代數公式定義了渦粘性系數，被稱為零方程模型。而我們熟知的k-epsilon模型及其變種（如k-omega模型等），也屬於渦粘性模型，該模型針對混合長度繼續演化，將其表示為湍動能k、湍流耗散率epsilon和湍流脈動速度的函數，而渦粘性系數便可由k和epsilon導出。普朗特之後，湍流的求解再次進入到了一個全新的時代，直至今日。

從無序中看到有序

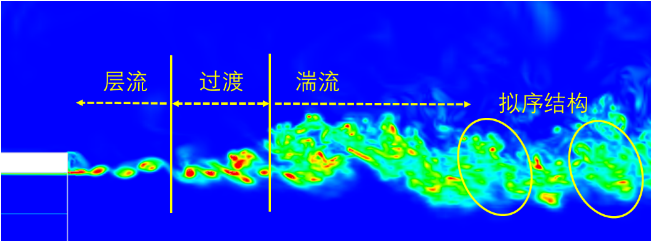
對於湍流來說，無論剛開始生成的大尺度渦有多豪橫，最後都會慢慢破碎成小渦，直至消亡。於是，湍流的無序中似乎又多了一份有序。1922年，愛寫詩的理查德森（Richardson）發現湍動能串級過程。大尺度渦從外界獲得能量並輸出給小尺度渦；小尺度渦則像一個耗能機械，把湍動能全部耗散為熱能；而流體的慣性猶如一個傳送機械，把大尺度渦的能量源源不斷的輸送給小尺度的渦。

1935年，泰勒開始研究更理想化的湍流。他在風洞實驗的均勻氣流後設置了幾排規則的格柵，均勻氣流流過格柵時便產生不規則擾動。這種不規則擾動向下遊運動過程中，由於沒有外界幹擾，逐漸演化為各向同性湍流。

湍流理論的築橋人

有了湍流能級串的定性認識和泰勒的均勻各向同性理論，深知“萬物皆可統計”的柯爾莫果洛夫敏銳的認識到湍流也可統計。於是柯大俠就使出了“統計大法”的第一招，即柯爾莫果洛夫的第一相似性假設：如果小渦的尺度足夠小，那麼它是無法直接感受到各向異性的大渦的，因此小尺度的渦可以認為是局部各向同性的，也就是說，能級串中各級傳遞特征相似，且由於此尺度范圍內粘性幾乎不起作用，因此傳遞速度相同，並等於最終的能量耗散率ε。

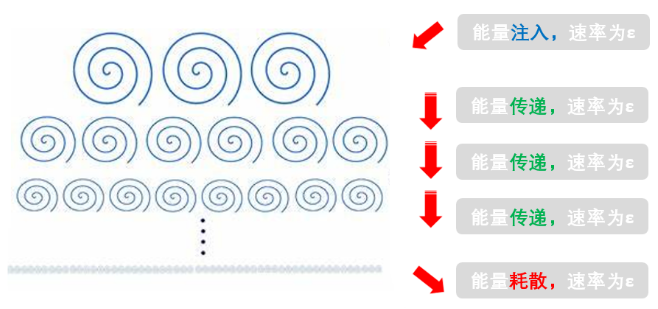
為了進一步的揭示湍流的奧秘，柯大俠緊接著使出了第二招，即第二相似性假設：對於尺度為G的流動結構，如果η<<G<<L（其中η為耗散尺度，L為宏觀尺度），那麼此尺度范圍的渦不僅不受大尺度各向異性的渦的影響，也不受耗散尺度的渦的影響，而其含能僅取決於能量傳遞速率ε，與粘性也無關。

最後，柯大俠使出了一招平平無奇的量綱分析，在1941年提出了湍流世界最著名的-5/3冪律，並在眾多學者的實驗中得到了驗證。當然隨著湍流理論的不斷發展，人們也發現了柯大俠的K41理論並非完美無缺，不過這並不妨礙它成為湍流研究史中最耀眼的一章。

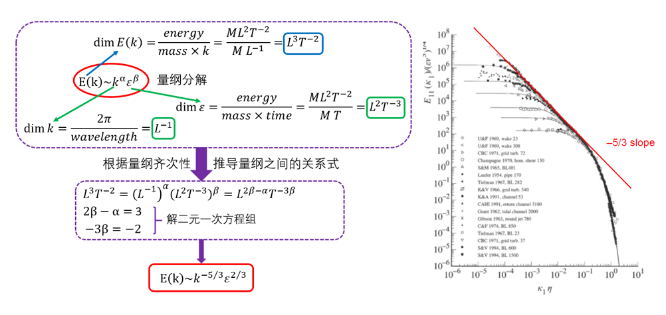
柯大俠的理論不僅開啟湍流理論研究的新篇章，也為後世使用LES和類LES方法求解湍流提供了理論依據。