在春秋戰國時期，華夏大地上湧現出了很多著名的學派並流傳至今，而後人也把這個思想文化迸發、群星閃耀的局面稱為“百家爭鳴”。回到我們最熟悉的CFD領域，作為RANS方法能夠生存的最重要基石，無數的學者提出了各種各樣的湍流模型，可謂百花齊放。可是迄今為止，仍然沒有一款湍流模型能夠一統天下，於是，在各種CFD軟件中下拉湍流模型選項的時候也總是能看到很多種選擇，這讓有選擇困難症的小夥伴們非常無奈。今天，我們就和大家一起聊一聊湍流模型的百家爭鳴。

　　01計算流體力學的門縫

　　我們在前面的文章中說過，因為湍流本身的無序和非定常性，N-S方程雖然在理論上可以描述湍流，但是實際上卻無法求解。直到1883年，雷諾通過經典的染色實驗讓人們親眼目睹了‘速度’這一物理變量的複雜性，而速度紊亂的時空演化本質上就是N-S方程的實際解。人們似乎看到了流動源頭，不過湍流本身的複雜性卻排山倒海般攔在所有人面前。

　　幸好對於大部分工程問題，我們並不需要完全求解湍流。比如工程上更關心流動的壓力損失和平均速度分布，而非湍流的細節。實驗做完五年以後，雷諾幡然醒悟：既然流動未可知，不妨使用統計學的思想——對N-S方程進行平均，把瞬時速度u分解為時均速度ū和脈動速度u’，代入N-S方程即可得到雷諾平均的N-S方程，也就是RANS。

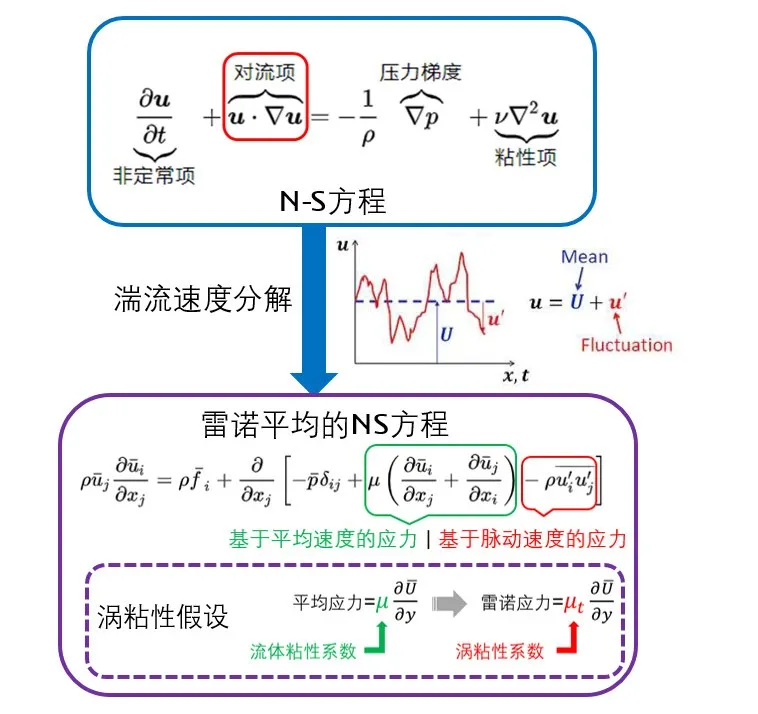
　　然而雷諾平均的N-S方程似乎更複雜了，除了平均速度的應力，上式中還多了脈動應力項，稱之為雷諾應力，成為新的攔路虎。不過冥冥之中自有天意，在雷諾提出對N-S方程進行平均的十年前， Boussinesq 已經將湍流脈動引起的切應力類比成了牛頓內摩擦定律，即用粘度乘以速度梯度來表示湍流脈動引起的切應力，這就是大名鼎鼎的渦粘性假設：雷諾應力=μt*(əū/əy)，其中的μt為渦粘性系數。至此，通往計算流體力學的大門終於打開了一條細縫。

　　02湍流模型的破局

　　縫隙雖開，人們還是擠不進去——對於絕大部分情況，μt 是未知的，而且渦粘性在邊界層附近變化很大。直到咱們廣義的祖師爺普朗特於1924年提出了混合長度理論，湍流的計算從數學表達到工程應用這座橋梁才逐漸變得清晰。

　　流體的粘性來自於分子自由運動產生的摻混，與分子自由程密切相關;對於渦粘性，也可以定義類似的參數。於是，普朗特定義混合長度l為湍流脈動摻混的長度，其物理意義為流體微團耗散前所經曆的距離。

　　於是，脈動速度可以表示為混合長度與壁面法向速度梯度的乘積，而渦粘性系數則可以相應的表述為μt=ρl2 *(əū/əy)。只要知道了混合長度，便可以明確渦粘性系數，進而求解RANS方程。

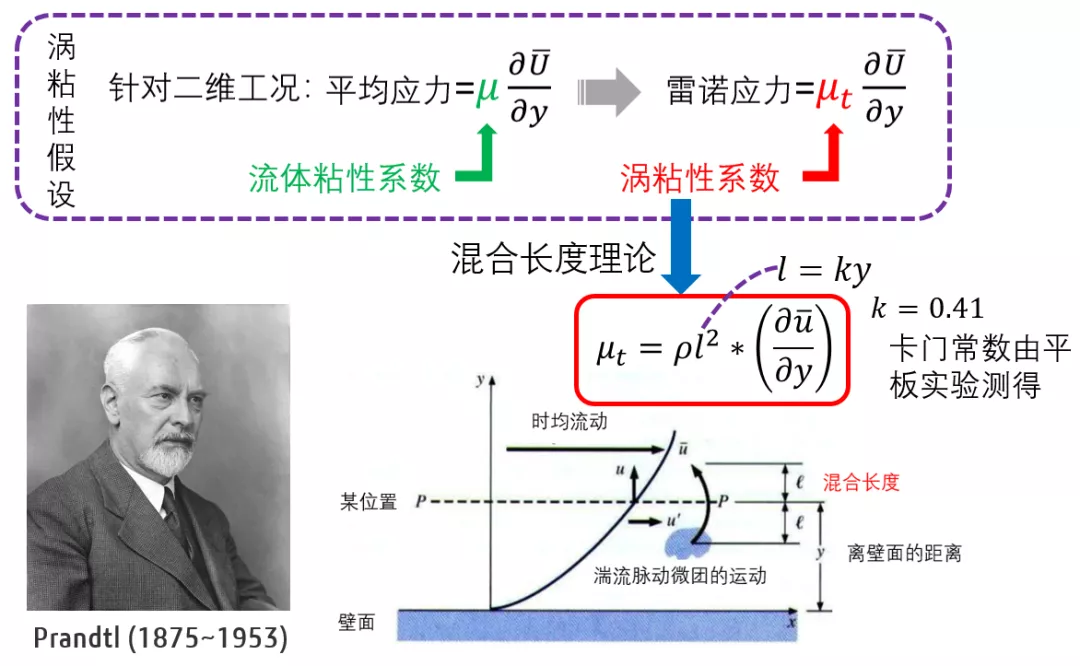
　　然而混合長度的准確值也很難得知，於是普朗特繼續發揚“跟著感覺走，天下在我手”的科學精神，大膽的認為混合長度與到壁面的距離成正比，從而得到了CFD領域第一個實用的渦粘模型。盡管普朗特的理論有東拼西湊的嫌疑，但是它使得湍流模型和計算流體力學實現了真正意義上的破局，並引領了其後近百年時光的CFD大發展。

　　03零方程模型的演化

　　普朗特的混合長度模型是代數模型，相當於直接用代數公式定義了渦粘性系數，被稱為零方程模型，即不引入額外的方程即可求解雷諾平均的N-S方程。小夥伴們都知道流動的邊界層是很複雜的，從內層到外層的流動狀態或者速度的分布也有很大的差異，普朗特用一個簡單的線性公式來表示混合長度確實不夠完善。

　　1978年， NASA Ames研究中心的Baldwin和Lowmax在AIAA第16屆航空航天科學會議上發表經典的論文《Thin Layer Approximation and Algebraic Model for Separated Turbulent Flows》，提出了一種更合理的混合長度模型。

　　Baldwin和Lowmax基於湍流邊界層內外層的流動差異，將湍流粘性系數也相應的定義成了兩個公式。內層延續普朗特的理論，而外層使用了更加符合實際的Clauser公式。當然在實際使用中，兩位學者也做了一些更新。後來很多學者使用B-L模型計算了翼型的繞流、平板流動、台階流，甚至是超聲速的流動，仿真結果和實驗都呈現比較好的一致性。

　　作為一種典型的代數模型，B-L模型不需要引入額外的方程即可求解RANS方程，其計算量較小，因此很多商用CFD軟件仍然會在湍流模型庫中保留B-L模型。不過需要特別說明的是，B-L模型只適用於小曲率、無分離的流動，不適合分離流、噴流或逆壓梯度較大的流動。

　　04備受矚目的k-epsilon模型

　　零方程模型看似化繁為簡，卻也逃不過嚴謹的流體力學家的吐槽——該模型通過簡單的公式定義渦粘性系數，而忽略了湍流複雜運動的本質。是時候翻翻舊賬了：在20世紀早期人們發現了湍流能級串的現象，1941年前蘇聯數學家Kolmogorov又提出了湍流能量譜理論，人們慢慢理解了湍動能的生成和耗散的規律。

　　前人栽樹，後人乘涼。於是一種攜帶著湍流演化思想的湍流模型便應運而生了，那便是兩位CFD領域的頂級大神B.E. Launder和D.B. Spalding以及他們的博士生們在20世紀70年代初陸續提出來的k-epsilon模型。

　　k-epsilon模型也屬於渦粘性模型，不過它變換了另外一種更加湍流的思想來求解混合長度，進而求解渦粘性系數：Kolmogorov的各向同性假設告訴我們湍流脈動速度u'=v'=w'，因此湍動能k則可簡化為3/2*u'2，而另外一個重要的參數epsilon表示流體微團的耗散率，即湍動能/耗散時間。

　　而定義為流體微團耗散前所經過距離的混合長度l，則可以順勢定義為耗散時間和流體微團速度的乘積。當然流體微團的速度和脈動速度是相當的，通過經驗系數來表示，於是我們可以用湍動能和湍流耗散率來表示湍流粘性系數。

　　面對多出來的兩個未知量k和epsilon，則分別建立其輸運方程進行封閉，這便是我們熟悉的k方程和epsilon方程。不過需要特別指出的是補充的epsilon方程中包含了經驗系數，這些系數一般由實驗得出，因此限制了k-epsilon模型的適用范圍。實際工程應用中，也有很多工程師會根據特定的應用場景修改相應的經驗參數來匹配實驗的結果。

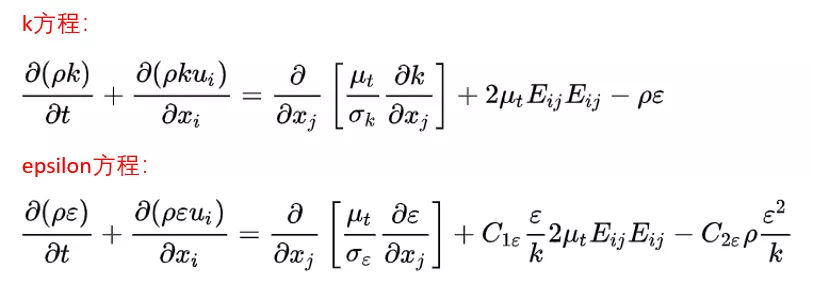
　　k-epsilon模型是對混合長度理論的進一步發展，因此相對於零方程模型適用於更複雜的流動。不過通過上述的推導，大家也可以看出來k-epsilon模型仍然有拼湊的嫌疑。它建立於湍流各向同性假設基礎之上，因此適合於完全發展的湍流，但不適用於逆壓梯度較高的流動，以及噴流和二次流。因此還有學者提出了Realizable 以及RNG k-epsilon模型，在壁面邊界層的處理以及分離流動的求解有了明顯的增強。

　　05寄於厚望的k-omega & SST模型

　　作為流傳最廣以及變種最多的湍流模型，k-epsilon模型的家族成員迄今為止仍然活躍在各大CFD軟件之中。不過愛折騰的人類怎能放過展示自己的機會呢，為了改善k-epsilon模型在求解逆壓梯度的流動中的計算精度問題，眾多學者做了很多嘗試。其中1988年，CFD大神Wilcox提出的k-omega模型被給予了很大的期望，並一路演化，在2006年，由Wilcox自己做了進一步的更新，形成了今天成熟的k-omega模型。

　　該模型定義了比耗散率omega，並通過k和omega來描述湍流粘性系數。從方程結構來看，omega方程和epsilon方程非常相似，但是兩者之間有一個重要的區別——epsilon方程中的經驗系數來源於粘性底層中的阻尼函數，而omega方程中的經驗系數卻不需要。這個阻尼函數的精度在強逆壓梯度的流動中存在一定的精度問題，因此k-epsilon模型不適合於處理逆壓梯度較大的流動，而k-omega模型卻能夠很好的駕馭。

　　此處需要特別指出的是，如果把omega的表達式直接代入epsilon方程，直接推導出來的方程比omega方程多了一個交叉擴散項，而這一項正是兩者之間的差異來源。

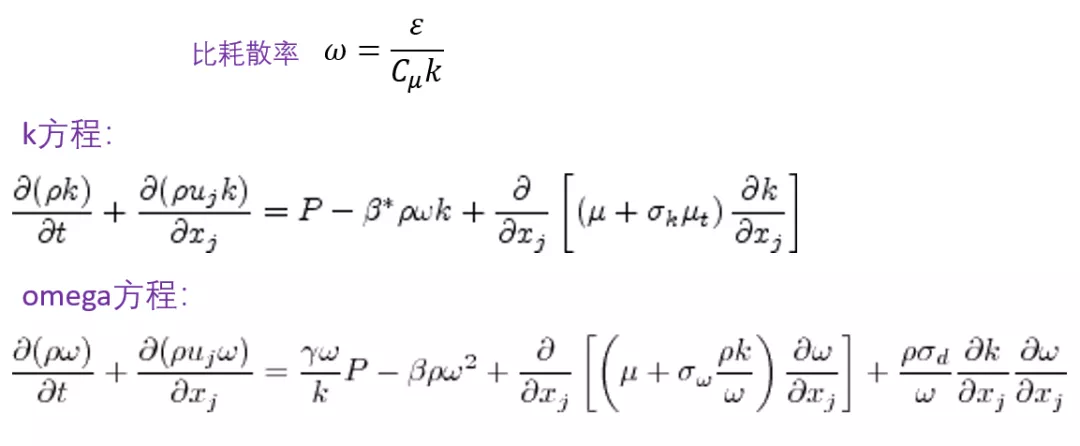
　　k-omega模型的確能夠很好的改善強逆壓梯度附近的流動求解，但是它也存在一個比較明顯的缺陷：當自由來流中湍動能出現微小的變化時，湍流粘度系數會出現劇烈的變化，導致流動的計算出現明顯的不合理;同時表面摩擦系數也會出現一定的變化，影響分離位置的判斷。反觀k-epsilon湍流模型對於自由來流的湍動能變化則沒有那麼敏感。

　　既然k-omega和k-epsilon各有所長，那就把它們結合起來吧，於是一個更加適用的湍流模型就誕生了。1992年，NASA Ames研究中心的Menter博士提出了著名的k-omega SST湍流模型，在omega方程後面添加了一個交叉擴散項，這個交叉擴散項剛好就是k-omega和k-epsilon模型之間的差異，而Menter博士則聰明的在這個交叉擴散項上面乘了一個混合函數，通過混合函數則可以輕易的控制湍流模型的變身：當混合函數為1時，omega方程還是omega方程，用於邊界層附近的求解，而當混合函數為0時，omega方程則變身成了epsilon方程，用於主流的求解，當然兩者之間通過一個混合區域來進行更加光順的過渡。

　　憑借著更好的適用性和計算精度，k-omega SST模型成為了越來越多的CFD工程師的選擇，尤其在航空航天和葉輪機械領域的出鏡率極高。

　　06特立獨行的一方程模型

　　既然有零方程模型和兩方程模型了，那中間的一方程呢?

　　一方程模型當然是有的，只是它並非是零和二之間的過渡，而是另外一種更加特立獨行的湍流模型。波音公司的大神Spalart基於翼型計算的豐富經驗，於1994年和Allmaras一起提出了著名的S-A模型。該模型不再使用湍動能和湍流耗散率計算渦粘性系數，而是直接導出渦粘性系數的輸運方程。

　　這種模式更適合於平均流場中有劇烈變化的湍流，比如幾何曲率明顯變化、存在激波等工況，因此廣泛應用於航空航天和葉輪機械領域。不過標准的S-A模型並沒有針對一般工業流域的流動進行校准，尤其是某些自由剪切流動比如平面射流，可能會產生較大的誤差。因此，它是一種更專用的湍流模型。

　　07朱砂痣 or 蚊子血?

　　作為RANS方法最重要的基石，湍流模型伴隨著CFDer們一起進步和成長。但因為RANS方法天然上忽略了湍流非定常的本質，使得湍流模型無論如何七十二變，都似乎難以抓住湍流這只頑猴。也難怪陪伴了CFDer這麼久，湍流模型卻時常被拍在牆上變成了一抹蚊子血。

　　不過筆者倒是更願意相信，隨著硬件和CFD方法的提升，LES甚至是DNS會慢慢融入並替代現在的RANS。到那時，或許我們會時長懷念起曾經和這些湍流模型一起掙紮的歲月，而這些湍流模型也會因為我們的懷念而變成胸口的朱砂痣。

　　-END-

　　普朗特（天津）工程技術有限公司是自主研發設計生產高端的流體力學實驗設備，水洞、風洞、水槽、金屬蜂窩, 示蹤粒子，竭誠為高校、科研院所和研發型企業服務。資訊熱線：15620639295